Two largest known prime numbers discovered just two weeks apart, one qualifies for $100k prize
Thursday, September 18, 2008
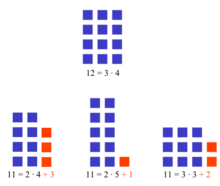
Image: Fredrik Johansson.
Two new records for the largest known prime number have been set, both breaking the 10 million digit threshold. On August 23, Edson Smith, a systems engineer for the Program in Computing laboratory at the University of California, Los Angeles in California, United States, confirmed the primality of the number through his work as a volunteer in the distributed computing project known as the Great Internet Mersenne Prime Search, or GIMPS. This new prime number is expressed as two to the 43,112,609th power minus one, and consists of 12,978,189 decimal digits when written out. This number qualifies GIMPS for a $100,000 award from the Electronic Frontier Foundation (EFF), offered to the first person or group to discover a prime number of 10 million digits or more. According to GIMPS' prize agreement, $50,000 will be given to the UCLA Department of Mathematics, $25,000 will be given to charity, $20,000 will be split among previous discoverers of Mersenne primes, and GIMPS will keep the remainder for funding and other uses. Smith, who was contacted by Scientific American by phone, said that the discovery was "quite unexpected."
Just two weeks later, on September 6, another Mersenne prime was discovered, this time by German electrical engineer Hans-Michael Elvenich, who worked for the chemical company Lanxess in Germany. This number is expressed as two to the 37,156,667th power minus one, and is 11,185,272 digits long. However, since this prime number was discovered later than the one found on August 23, it does not qualify for the EFF prize. Elvenich said that it was a "finally a great success" after having participated in GIMPS for four years.
A prime number is a positive integer that can be evenly divided only by 1 and itself. For example, 2, 3 and 11 are prime numbers. 21 is not a prime number because it is a product of 3 and 7. These types of prime numbers are called Mersenne primes, which can be expressed as one less than a power of two. Mersenne primes are rare, and only 46 are known up to now. The first few Mersenne primes are 3, 7, 31, 127 and 8191.
These numbers took a total of several weeks to verify, using different software and hardware. Each number was independently checked by several members of GIMPS' verification team, using 16-core systems of different configurations. The two primes were announced by GIMPS on September 16. Before these two discoveries, the two previously largest known prime numbers were discovered by UCMO professors Curtis Cooper and Steven Boone in Missouri, United States, and their record lasted almost three years. Historically, prime numbers discovered by GIMPS are larger than the one previously found. The only other exception was when the 29th Mersenne prime was discovered after the 30th and 31st were found.
Founded by M.I.T. graduate George Woltman in 1996, GIMPS has found 12 Mersenne primes, or about one per year on average. Volunteers who wish to help find primes can download a program called Prime95, which runs in the background.
Smaller prime numbers, such as those with a few hundred digits, are often used in cryptography. The recently discovered prime numbers are too large to have much practical value, although it is believed by some that such prime numbers may still have undiscovered uses. However, mathematics enthusiasts often seek them for fun, and the GIMPS community is already looking forward to finding a 100 million digit prime that will qualify for a $150,000 prize from the EFF.
Related news
- "CMSU computing team discovers another record size prime" — Wikinews, September 11, 2006
- "Distributed computing discovers largest known prime number" — Wikinews, December 30, 2005
Sister links
Sources
- Press Release: "GIMPS press release" — Great Internet Mersenne Prime Search, September 16, 2008
- John Matson. "Big and bigger: New prime numbers claim top two spots" — Scientific American, September 16, 2008
- Eric W. Weisstein. "45th and 46th Mersenne Primes Found" — Wolfram Research, September 16, 2008

